二分查找
二分法查找
题目链接:https://leetcode-cn.com/problems/binary-search/
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
思路
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找返回的元素下标就可能不是唯一的。这些都是使用二分法的前提条件,当看到题目描述满足上述条件的时候,需要想一想是否可以使用二分法。
二分法查找涉及很多边界条件,逻辑比较简单。但需要考虑清楚对区间的定义,即区间的定义就是不变量。要在二分法查找的过程中,保持不变量,就是在 while 寻找中每一次边界的处理都要坚持根据区间的定义来操作,这即为循环不变量规则。
写二分法,区间定义一般为两种,左闭右闭即[left,right],或者左闭右开即[left,right)。
二分法第一种写法
第一种写法,我们定义target是在一个左闭右闭的区间内,即[left,right](重点)
区间的定义决定了二分法的代码该如何写,因为定义target在[left,right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为 left == right 是有意义的。
- if (nums[middle] > target),则 right 要赋值为middle - 1,因为当前这个 nums[middle] 一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1。
例如在数组 1,2,3,4,7,9,10 中查找元素2,如图所示:
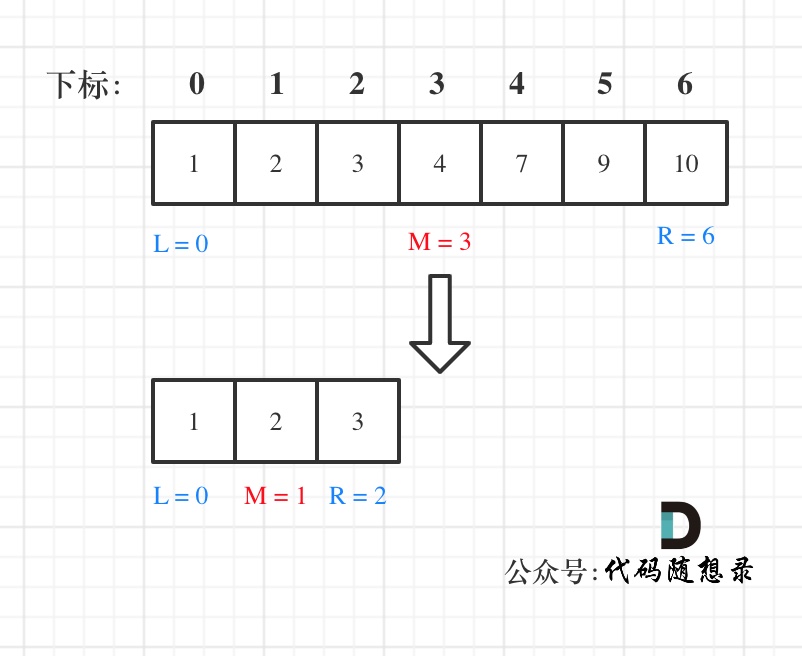
1 | class Solution { |
二分法第二种写法
如果说定义target是在一个左闭右开的区间内,即 [left,right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right), 这里使用 <, 因为left == right在区间[left,right)是没有意义的。
- if (nums[middle] > target),则 right 更新为middle,因为当前nums[middle]不等于target,去左区间将继续寻找,而寻找区间是左闭右开区间,所以 right 更新为 middle,即:下一个查询区间不会去比较 nums[middle]。
在数组 1,2,3,4,7,9,10 中查找元素2,如图所示:(注意和方法一的区别)
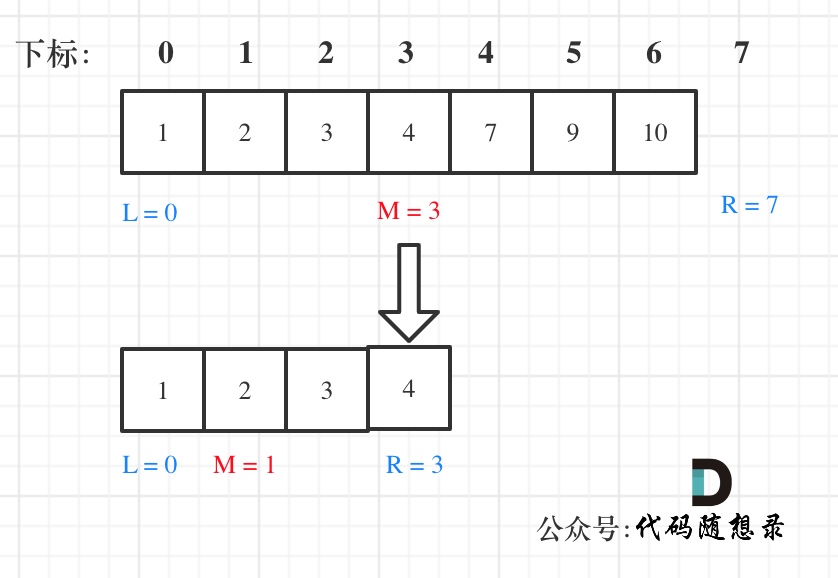
1 | // 版本二 |
总结
二分法需要理解清楚区间定义,处理好边界。
区间的定义就是不变量,在循环中坚持根据查找区间的定义来做边界处理,即循环不变量规则。







