算法基础之贪心算法(一)
905. 区间选点
给定 N 个闭区间 [ ai, bi ],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai, bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需的点的最小数量。
数据范围
输入样例:
1 | 3 |
输出样例:
1 | 2 |
AC
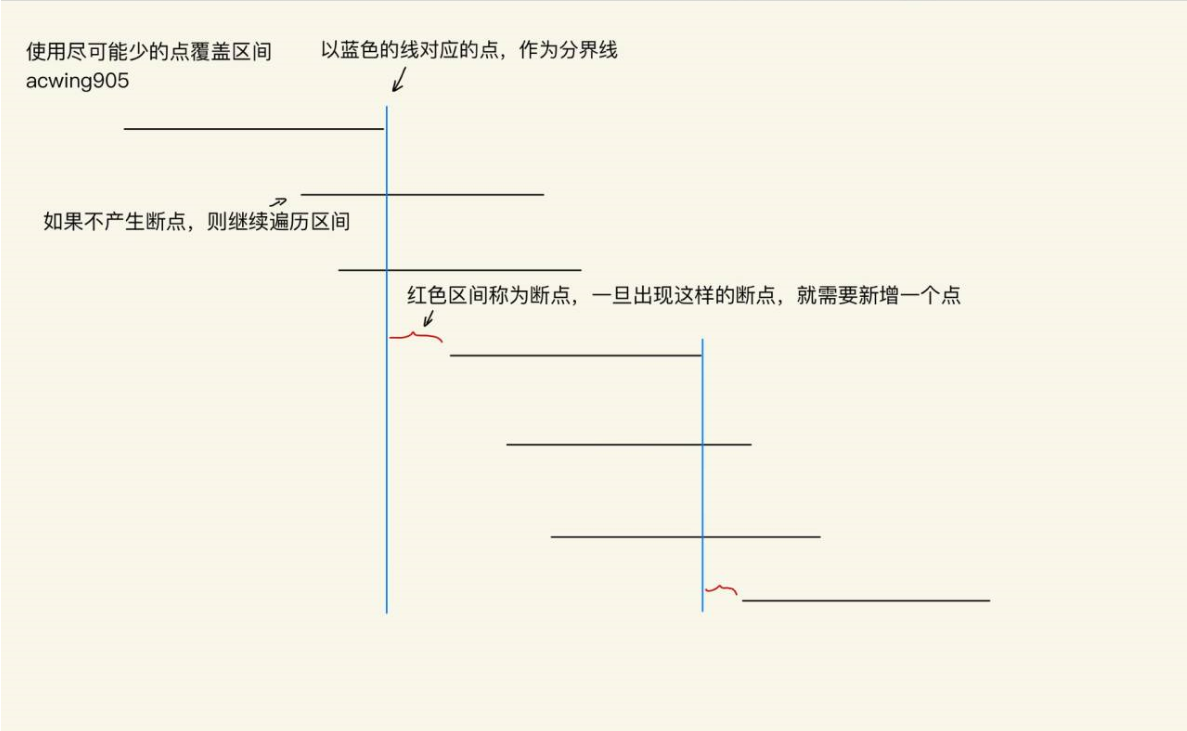
将每个区间按照右端点从小到大进行排序
从前往后枚举区间,end 值初始化为无穷小
如果本次区间不能覆盖上次区间的右端点,即
ed < range[i].l则需要选择一个新的点,
res ++ ; ed = range[i].r;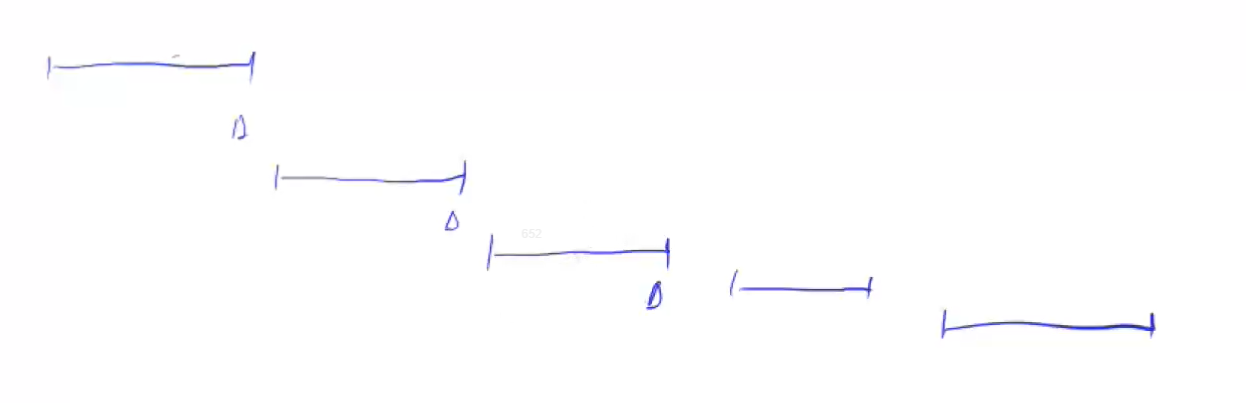
如果本次区间可以覆盖上次区间的右端点,则进行下一轮循环
时间复杂度 O(nlogn)
证明
证明 ans <= cnt : cnt 是一种可行方案, ans 是可行方案的最优解,也就是最小值
证明 ans >= cnt : cnt 是可行方案的一个区间集合,区间从小到大排序,两两间不相交
所以覆盖每一个区间至少需要 cnt 个点
1 |
|
评论
Va