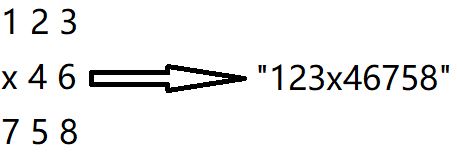搜索与图论（一）

DFS 深度优先搜索

842. 排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1 ≤ n ≤ 7

输入样例：

输出样例：

AC

此题采用 DFS 深度优先搜索，也即典型回溯算法。回溯的本质是穷举，但可以加上一些剪枝操作来高效一些。

DFS（回溯算法）解决的问题

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

DFS 遍历过程

DFS 算法模板框架

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        dfs(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

如何用 dfs 解决全排列

对于全排列问题，以 n = 3 为例，搜索顺序为下：

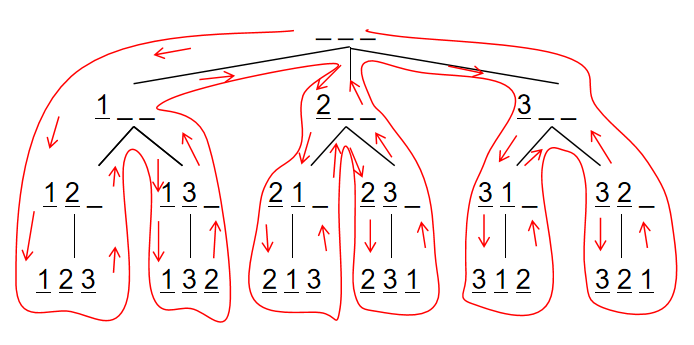
每次进行到尽头，并回溯走向下一个分支。

代码

#include <iostream>

using namespace std;

const int N = 10;

int path[N]; // 保存序列
int state[N]; // 数字状态，是否被用过

int n;

void dfs(int u) {
    if (u > n) { // 数字填完，排序遍历完成，输出
        for (int i = 1; i <= n; i++) {
            cout << path[i] << ' ';
        }
        cout << endl;
    }
    
    for (int i = 1; i <= n; i++) { // 空位可选择的数字为：1 ~ n
        if (!state[i]) { // 如果数字 i 没有被使用过
            path[u] = i; // 放入空位
            state[i] = 1; // 修改该数字状态
            dfs(u + 1); // 递归，填入下一位数字
            state[i] = 0; // 回溯，取出 i
        }
    }
}

int main() {
    cin >> n;
    dfs(1);
    
    return 0;
}

843. n-皇后问题

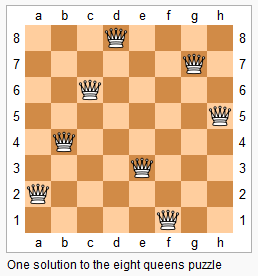
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1 ≤ n ≤ 9

输入样例：

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

AC

思路

皇后们的约束条件：

不能同行
不能同列
不能同斜线

按行单层搜索，其中 col[x],dg[x + y], udg[n + y - x] 分别记录的是该位置的列，斜，反斜线上是否已经存在过，若均不存在，填入皇后，并递归到下一行

代码分析

#include <iostream>

using namespace std;

const int N = 20;

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// board[N][N]用来存路径

int n;
char board[N][N]; 
bool col[N], dg[N], udg[N]; 

void dfs(int u) {
    // 判断是否已经搜了 n 行，则打印输出
    if (u == n) {
        for (int i = 0; i < n; i++) {
            cout << board[i] << endl;
        }
        cout << endl;
        
        return;
    }
    
    // 逐行搜索
    for (int i = 0; i < n; i++) {
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        // udg[n + i - u]，+n 是为了保证下标非负
        if (!col[i] && !dg[u + i] && !udg[n + i - u]) {
            // 满足条件存储
            board[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n + i - u] = true;
            
            dfs(u + 1); // 递归
            
            // 还原现场
            col[i] = dg[u + i] = udg[n + i - u] = false;
            board[u][i] = '.';
        }
    }
}


int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            board[i][j] = '.';
        }
    }
    
    dfs(0);
    
    return 0;
}

BFS 广度优先搜索

844. 走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n , m≤100

输入样例：

输出样例：

AC

思路

思路：

用 g[n][m] 存储地图，f[n][m] 存储起点到 n,m 的距离。
从起点开始广度优先遍历地图。
当地图遍历完，就求出了起点到各个点的距离，输出f[n][m] 即可。

代码

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

typedef pair<int, int> PII; // 以下标为坐标成对存储

const int N = 110;

int g[N][N]; // 存储地图
int f[N][N]; // 存储距离

int n, m;

void bfs(int a, int b) {
    queue<PII> q; // 将坐标按照队列存入
    q.push({a, b}); // 存入当前点
    
    while (!q.empty()) { // 队列中有坐标时
        PII start = q.front(); // 起点
        q.pop(); // 用过的坐标出队列
        g[start.first][start.second] = 1; // 走过的防止回头
        int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0}; // 四个方向
        for (int i = 0; i < 4; i++) {
            int x = start.first + dx[i], y = start.second + dy[i]; // 坐标 + 移动方向
            if (g[x][y] == 0) { // 如果这条路没有走过
                g[x][y] = 1;
                f[x][y] = f[start.first][start.second] + 1; // 从当前点走过去，距离等于当前距离+1
                q.push({x, y}); // 入队列
            }
        }
    }
    cout << f[n][m];
}

int main() {
    memset(g, 1, sizeof g); // 初始化地图外圈，即可不用做越界判断
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> g[i][j];
        }
    }
    
    bfs(1, 1);
    
    return 0;
}

845. 八数码

在一个 3×3 的网格中，1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。

例如：

1
2
3

1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1
2
3

1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1
2
3

1 2 3   1 2 3   1 2 3   1 2 3
x 4 6   4 x 6   4 5 6   4 5 6
7 5 8   7 5 8   7 x 8   7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将 3×3 的初始网格描绘出来。

例如，如果初始网格如下所示：

1
2
3

1 2 3 
x 4 6 
7 5 8

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出 −1。

输入样例：

1	2 3 4 1 5 x 7 6 8

输出样例

AC

思路

题目目标
移动情况

移动方式：

将每一种情况作为1个节点，目标情况即为终点

从初始状况移动到目标情况 —> 求最短路
难点

第一点：怎么表示一种情况使其能作为节点？

第二点：如何记录每一个状态的“距离”（即需要移动的次数）？

第三点：队列怎么定义，d 数组怎么定义？

解决方案

将 “3*3矩阵” 转化为 “字符串”

队列可以用 queue<string>
//直接存转化后的字符串
d数组用 unordered_map<string, int>
//将字符串和数字联系在一起，字符串表示状态，数字表示距离

矩阵与字符串的转换方式

代码

#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

int bfs(string start) {
    string end = "12345678x"; // 目标状态
    
    queue<string> q; 
    unordered_map<string, int> d;
    
    // 初始化
    q.push(start);
    d[start] = 0;
    
    int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1}; // 移动方向
    
    while (q.size()) { // 队列不为空时
        auto t = q.front(); // 获取队头坐标
        q.pop(); 
        
        int dance = d[t]; // 记录当前距离
        if (t == end) { // 如果已经是最终状态，则返回距离
            return dance;
        }
        
        int k = t.find('x'); // 查询 x 在字符串中的下标 
        int x = k / 3, y = k % 3; // 转换为矩阵中的坐标
        
        for (int i = 0; i < 4; i++) { // 四个方向移动
            int a = x + dx[i], b = y + dy[i]; // 移动后的坐标
            if (a >= 0 && a < 3 && b >= 0 && b < 3) { // 若没有出界
                swap(t[k], t[a * 3 + b]); // 交换相应位置的数
                
                if (!d.count(t)) { // 若当前状态为第一次遍历，则记录记录，入队
                    d[t] = dance + 1;
                    q.push(t);
                }
                
                swap(t[k], t[a * 3 + b]); // 恢复现场，为下次做准备
            }
        }
    }
    
    return -1; // 无法转换到目标
}

int main() {
    string c, start;
    
    for (int i = 0; i < 9; i++) {
        cin >> c;
        start += c;
    }
    
    cout << bfs(start) << endl;
    
    return 0;
    
}

树与图的深度优先遍历

846. 树的重心

给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 n，表示树的结点数。

接下来 n−1 行，每行包含两个整数 a 和 b，表示点 a 和点 b 之间存在一条边。

输出格式

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

1 ≤ n ≤ 105

输入样例

输出样例：

AC

（数组建立邻接表）树的 dfs

//邻接表
int h[N], e[N * 2], ne[N * 2], idx;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

树的 bfs 模板

// 需要标记数组st[N],  遍历节点的每个相邻的便
void dfs(int u) {
    st[u] = true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            dfs(j);
        }
    }
}

本题的本质是树的 dfs，每次 dfs 可以确定以u为重心的最大连通块的节点数，并且更新一下 ans。

也就是说，dfs 并不直接返回答案，而是在每次更新中迭代一次答案。

这样的套路会经常用到，在树的 dfs 题目中

代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边

int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入，n个节点
int ans = N; //表示重心的所有的子树中，最大的子树的结点数目

bool st[N]; //记录节点是否被访问过，访问过则标记为true

//a所对应的单链表中插入b  a作为根 
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// dfs 框架
/*
void dfs(int u){
    st[u]=true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(!st[j]) {
            dfs(j);
        }
    }
}
*/

//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) {
    int res = 0; //存储 删掉某个节点之后，最大的连通子图节点数
    st[u] = true; //标记访问过u节点
    int sum = 1; //存储 以u为根的树 的节点数, 包括u，如图中的4号节点

    //访问u的每个子节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        //因为每个节点的编号都是不一样的，所以 用编号为下标 来标记是否被访问过
        if (!st[j]) {
            int s = dfs(j);  // u节点的单棵子树节点数 如图中的size值
            res = max(res, s); // 记录最大联通子图的节点数
            sum += s; //以j为根的树 的节点数
        }
    }

    //n-sum 如图中的n-size值，不包括根节点4；
    res = max(res, n - sum); // 选择u节点为重心，最大的 连通子图节点数
    ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的 节点数
    return sum;
}

int main() {
    memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
    cin >> n; //表示树的结点数

    // 题目接下来会输入，n-1行数据，
    // 树中是不存在环的，对于有n个节点的树，必定是n-1条边
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); //无向图
    }

    dfs(1); //可以任意选定一个节点开始 u<=n

    cout << ans << endl;

    return 0;
}

树与图的广度优先遍历

847. 图中点的层次

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环。

所有边的长度都是 1，点的编号为 1∼n。

请你求出 1 号点到 n 号点的最短距离，如果从 11 号点无法走到 n 号点，输出 −1。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 a 和 b，表示存在一条从 a 走到 b 的长度为 1 的边。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

数据范围

1 ≤ n,m ≤ 105

输入样例：

输出样例：

AC

思路

用 d 数组保存1号节点到各个节点的距离，初始时，都是无穷大。

用 st 数组标记各个节点有没有走到过。

从 1 号节点开始，广度优先遍历：

1 号节点入队列，d[1] 的值更新为 0。
如果队列非空，就取出队头，找到队头节点能到的所有节点。如果队头节点能到走到的节点没有标记过，就将节点的d值更新为队头的d值+1，然后入队。
重复步骤 2 直到队列为空。
这个时候，d数组中就存储了 1 号节点到各个节点的距离了。如果距离是无穷大，则不能到达，输出 -1，如果距离不是无穷大，则能到达，输出距离。
图的存储：邻接表
用 h 数组保存各个节点能到的第一个节点的编号。开始时，h[i] 全部为 -1。
用 e 数组保存节点编号，ne 数组保存 e 数组对应位置的下一个节点所在的索引。
用 idx 保存下一个 e 数组中，可以放入节点位置的索引
插入边使用的头插法，例如插入：a->b。首先把b节点存入e数组，e[idx] = b。然后 b 节点的后继是h[a]，ne[idx] = h[a]。最后，a 的后继更新为 b 节点的编号，h[a] = idx，索引指向下一个可以存储节点的位置，idx ++ 。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;

const int N = 100010;

int h[N],ne[N], e[N], idx;//邻接表数据结构
int d[N];//存储距离
int st[N];//标记点是否走到过
int n, m;

void add(int a, int b) { //邻接表存储图
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs() {
    memset(d, 0x3f, sizeof(d)); // 初始都没有走到过，距离无穷大
    d[1] = 0; // 从1号节点开始，距离为0
    queue<int> q; // 队列
    q.push(1); // 1号节点入队列
    while(q.size()) { // 对列非空，就一直往后搜索
        int t = q.front(); // 队头出队，找该点能到的点
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i]) { // 遍历所有t节点能到的点，i为节点索引
            int j = e[i]; // 通过索引i得到t能到的节点编号
            if(!st[j]) { // 如果没有遍历过
                d[j] = d[t] + 1; // 距离为t号节点的距离+1
                q.push(j); // 节点入队
                st[j] = 1; // 入队后标记，已经遍历过了
            }
        }
    }
}

int main()
{
    cin >> n >>m;
    memset(h, -1, sizeof h); // 初始化，所有节点没有后继，后继都是-1
    for(int i = 0; i < m; i++) { // 读入所有边
        int a, b;
        cin >> a >> b;
        add(a, b);//加入邻接表
    }
    bfs(); // 广度优先遍历

    //如果到n号节点的距离不是无穷大，输出距离，如果是无穷大，输出-1.
    if (d[n] == 0x3f3f3f3f) {
        cout << "-1" << endl;
    }
    else {
        cout << d[n] << endl;
    }
    
    return 0;
}

DFS 深度优先搜索

842. 排列数字

输入格式

输出格式

数据范围

输入样例：

输出样例：

AC

DFS（回溯算法）解决的问题

DFS 遍历过程

DFS 算法模板框架

如何用 dfs 解决全排列

代码

843. n-皇后问题

输入格式

输出格式

数据范围

输入样例：

输出样例：

AC

思路

代码分析

BFS 广度优先搜索

844. 走迷宫

输入格式

输出格式

数据范围

输入样例：

输出样例：

AC

思路

代码

845. 八数码

输入格式

输出格式

输入样例：

输出样例

AC

思路

代码

树与图的深度优先遍历

846. 树的重心

输入格式

输出格式

数据范围

输入样例

输出样例：

AC

（数组建立邻接表） 树的 dfs

树的 bfs 模板

代码

树与图的广度优先遍历

847. 图中点的层次

输入格式

输出格式

数据范围

输入样例：

输出样例：

AC

思路

代码

（数组建立邻接表）树的 dfs