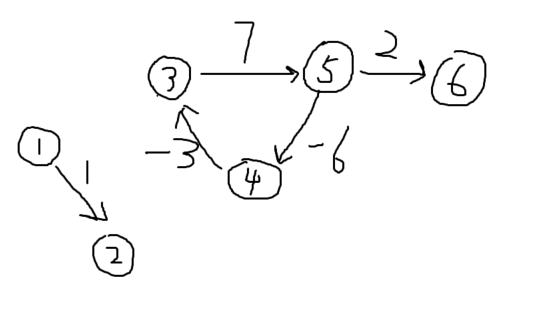
拓扑排序 848. 有向图的拓扑序列 给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
输入格式 第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y 的有向边 (x,y)。
输出格式 共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围 1 ≤ n, m ≤ 105
输入样例: 输出样例: AC 思路 只适用于 AOV网 (有向无环图)
有向无环图一定是拓扑序列,有向有环图一定不是拓扑序列。
算法流程:
将入度为 0 的店指向的边删掉,每次删掉后,将入度为 0 的点入队,则最后入队的点的顺序即是拓扑序列。
主要由以下两步循环执行,直到不存在入度为 0 的顶点为止
选择一个入度为 0 的顶点,并将它输出;
删除图中从顶点连出的所有边。
循环结束:
若输出的顶点数小于图中的顶点数,则表示该图存在回路,即无法拓扑排序,
否则,输出的就是拓扑序列 (不唯一)
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 #include <iostream> #include <algorithm> #include <cstring> using namespace std ;const int N = 100010 ;int h[N], e[N], ne[N], idx;int q[N], d[N];int n, m;void add (int a, int b) e[idx] = b; ne[idx] = h[a]; h[a] = idx++; } bool topsort () int hh = 0 , tt = -1 ; for (int i = 1 ; i <= n; i++) { if (!d[i]) { q[++tt] = i; } } while (hh <= tt) { int t = q[hh++]; for (int i = h[t]; i != -1 ; i = ne[i]) { int j = e[i]; if (--d[j] == 0 ) { q[++tt] = j; } } } return tt == n-1 ; } int main () cin >> n >> m; memset (h, -1 , sizeof h); for (int i = 0 ; i < m; i++) { int a, b; cin >> a >> b; add(a, b); d[b]++; } if (topsort()) { for (int i = 0 ; i < n; i++) { cout << q[i] << ' ' ; } } else { cout << "-1" << endl ; } return 0 ; }
Dijkstra 849. Dijkstra求最短路径 I 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 11 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式 第一行包含整数 n和 m。
接下来 mm 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式 输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围 1 ≤ n ≤ 500
输入样例: 输出样例: AC 思路 Dijkstra 算法即进行 n 次迭代去确定每个点到起点的最小值,最后输出的终点的即为要寻找的最短的距离
每次迭代过程都先找到未确定的最短距离的点中距离最短的点
通过上述操作当前我们的t代表就是剩余未确定最短路的点中 路径最短的点
然后用这个去更新其余未确定点的最短距离
但 Dijkstra 不适于边权重为负值的,如有后续再介绍。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <iostream> #include <algorithm> #include <cstring> using namespace std ;const int N = 510 ;int n, m;int g[N][N]; int dist[N]; bool st[N]; int dijstra () memset (dist, 0x3f , sizeof dist); dist[1 ] = 0 ; for (int i = 0 ; i < n; i++) { int t = -1 ; for (int j = 1 ; j <= n; j++) { if (!st[j] && (t == -1 || dist[t] > dist[j])) { t = j; } } for (int j = 1 ; j <= n; j++) { dist[j] = min(dist[j], dist[t] + g[t][j]); } st[t] = true ; } if (dist[n] == 0x3f3f3f3f ) { return -1 ; } return dist[n]; } int main () cin >> n >> m; memset (g, 0x3f , sizeof g); while (m--) { int x, y ,z; cin >> x >> y >> z; g[x][y] = min(g[x][y], z); } cout << dijstra() << endl ; return 0 ; }
850. Dijkstra求最短路 II 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式 第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式 输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围 图中涉及边长均不小于 0,且不超过 10000。
输入样例: 输出样例: AC 思路 优化版的 Dijkstra 是对朴素版 Dijkstra进行了优化,在朴素版 Dijkstra中时间复杂度最高的寻找距离最短的点O(n^2)可以使用最小堆优化。
一号点的距离初始化为零,其他点初始化成无穷大。
将一号点放入堆中。
不断循环,直到堆空。每一次循环中执行的操作为:
时间复杂度:
寻找路径最短的点:O(n)
加入集合S:O(n)
更新距离:O(mlogn)
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <iostream> #include <algorithm> #include <cstring> #include <queue> using namespace std ;typedef pair <int , int > PII;const int N = 1e6 + 10 ;int n, m;int h[N], e[N], ne[N], idx;int w[N]; int dist[N];bool st[N]; void add (int a, int b, int c) e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++; } int dijkstra () memset (dist, 0x3f , sizeof dist); dist[1 ] = 0 ; priority_queue <PII, vector <PII>, greater<PII>> heap; heap.push({0 , 1 }); while (heap.size()) { auto t = heap.top(); heap.pop(); int ver = t.second, distance = t.first; if (st[ver]) { continue ; } st[ver] = true ; for (int i = h[ver]; i != -1 ; i = ne[i]) { int j = e[i]; if (dist[j] > dist[ver] + w[i]) { dist[j] = dist[ver] + w[i]; heap.push({dist[j], j}); } } } if (dist[n] == 0x3f3f3f3f ) { return -1 ; } return dist[n]; } int main () cin >> n >> m; memset (h, -1 , sizeof h); while (m--) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } cout << dijkstra() << endl ; return 0 ; }
Bellman-Ford 853. 有边数限制的最短路 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数 。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 impossible。
注意:图中可能 存在负权回路 。
输入格式 第一行包含三个整数 n, m, k 。
接下来 m 行,每行包含三个整数 x, y, z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式 输出一个整数,表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
如果不存在满足条件的路径,则输出 impossible。
数据范围 任意边长的绝对值不超过 10000。
输入样例: 输出样例: AC 思路 在边权可正可负的图中,环有零环、正环、负环 3 种。如果包含零环或正环,去掉以后路劲不会变长;如果包含负环,则意味这最短路不存在。
既然不含环,最短路最多只经过(起点不算)n - 1 个结点,可以通过 n - 1 轮松弛操作得到,像这样(起点仍是0):
1 2 3 for n次 for 所有边 a,b,w (松弛操作) dist[b] = min(dist[b],back[a] + w)
注意:back[] 数组是上一次迭代后 dist[] 数组的备份,由于是每个点同时向外出发,因此需要对 dist[] 数组进行备份,若不进行备份会因此发生串联效应,影响到下一个点
时间复杂度 O(nm)
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <iostream> #include <algorithm> #include <cstring> using namespace std ;const int N = 510 , M = 10010 ;int n, m, k;int dist[N], back[N]; struct Edge { int a, b, w; }e[M]; void bellman_ford () memset (dist, 0x3f , sizeof dist); dist[1 ] = 0 ; for (int i = 0 ; i < k; i++) { memcpy (back, dist, sizeof dist); for (int j = 0 ; j < m; j++) { int a = e[j].a, b = e[j].b, w = e[j].w; dist[b] = min(dist[b], back[a] + w); } } if (dist[n] > 0x3f3f3f3f / 2 ) { puts ("impossible" ); } else { printf ("%d\n" , dist[n]); } } int main () cin >> n >> m >> k; for (int i = 0 ; i < m; i++) { int a, b, w; cin >> a >> b >> w; e[i] = {a, b, w}; } bellman_ford(); return 0 ; }
Spfa(队列优化的Bellman-Ford算法) 851. spfa求最短路 给定一个 nn 个点 mm 条边的有向图,图中可能存在重边和自环, 边权可能为负数 。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible。
数据保证不存在负权回路。
输入格式 第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x, y, z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式 输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围 图中涉及边长绝对值均不超过 10000。
输入样例: 输出样例: AC 思路 SPFA算法仅仅只是对该算法的一个优化。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 #include <iostream> #include <algorithm> #include <cstring> #include <queue> using namespace std ;const int N = 100010 ;int n, m;int h[N], e[N], w[N], ne[N], idx; int dist[N]; bool st[N]; void add (int a, int b, int c) e[idx] = b; ne[idx] = h[a]; w[idx] = c; h[a] =idx++; } int spfa () memset (dist, 0x3f , sizeof dist); dist[1 ] = 0 ; queue <int > q; q.push(1 ); st[1 ] = true ; while (q.size()) { int t = q.front(); q.pop(); st[t] = false ; for (int i = h[t]; i != -1 ; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; if (!st[j]) { q.push(j); st[j] = true ; } } } } return dist[n]; } int main () cin >> n >> m; memset (h, -1 , sizeof h); while (m--) { int x, y, z; cin >> x >> y >> z; add(x, y, z); } int t = spfa(); if (t == 0x3f3f3f3f ) { cout << "impossible" << endl ; } else { cout << t << endl ; } return 0 ; }
853. spfa判断负环 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数 。
请你判断图中是否存在负权回路。
输入格式 第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x, y, z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式 如果图中存在 负权回路,则输出 Yes,否则输出 No。
数据范围 图中涉及边长绝对值均不超过 10000。
输入样例: 输出样例: AC 思路 求负环的常用方法,基于SPFA,一般都用方法 2(该题也是用方法 2):
方法 1:统计每个点入队的次数,如果某个点入队n次,则说明存在负环
y总的原话
每次做一遍 spfa() 一定是正确的,但时间复杂度较高,可能会超时。初始时将所有点插入队列中可以按如下方式理解:
1、dist[x] 记录虚拟源点到x的最短距离
2、cnt[x] 记录当前 x 点到虚拟源点最短路的边数,初始每个点到虚拟源点的距离为 0,只要他能再走 n 步,即 cnt[x] >= n,则表示该图中一定存在负环,由于从虚拟源点到x至少经过 n 条边时,则说明图中至少有 n + 1个点,表示一定有点是重复使用
3、若 dist[j] > dist[t] + w[i], 则表示从t点走到j点能够让权值变少,因此进行对该点j进行更新,并且对应 cnt[j] = cnt[t] + 1 ,往前走一步
注意:该题是判断是否存在负环,并非判断是否存在从1开始的负环,因此需要将所有的点都加入队列中,更新周围的点
时间复杂度 一般:O(m)O(m) 最坏:O(nm)
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 #include <iostream> #include <cstring> #include <queue> using namespace std ;const int N = 2010 , M = 100010 ;int n, m;int h[N], e[M], ne[M], w[M], idx; int dist[N], cnt[N]; bool st[N]; void add (int a, int b, int c) e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++; } bool spfa () queue <int > q; for (int i = 1 ; i <= n; i++) { st[i] = true ; q.push(i); } while (q.size()) { int t = q.front(); q.pop(); st[t] = false ; for (int i = h[t]; i != -1 ; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; cnt[j] = cnt[t] + 1 ; if (cnt[j] >= n) { return true ; } if (!st[j]) { q.push(j); st[j] = true ; } } } } return false ; } int main () cin >> n >> m; memset (h, -1 , sizeof h); while (m--) { int x, y, z; cin >> x >> y >> z; add(x, y, z); } if (spfa()) { cout << "Yes" << endl ; } else { cout << "No" << endl ; } return 0 ; }
Floyd 854. Floyd求最短路 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式 第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x, y, z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
接下来 k 行,每行包含两个整数 x, y,表示询问点 x 到点 y 的最短距离。
输出格式 共 k 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出 impossible。
数据范围 图中涉及边长绝对值均不超过 10000。
输入样例: 1 2 3 4 5 6 3 3 2 1 2 1 2 3 2 1 3 1 2 1 1 3
输出样例: AC 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 #include <iostream> #include <algorithm> using namespace std ;const int N = 210 , INF = 1e9 ;int n, m, k;int d[N][N];void floyd () for (int k = 1 ; k <= n; k++) { for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= n; j++) { d[i][j] = min(d[i][j], d[i][k] + d[k][j]); } } } } int main () cin >> n >> m >> k; for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= n; j++) { if (i == j) { d[i][j] = 0 ; } else { d[i][j] = INF; } } } while (m--) { int x, y, z; cin >> x >> y >> z; d[x][y] = min(d[x][y], z); } floyd(); while (k--) { int x, y; cin >> x >> y; int t = d[x][y]; if (t > INF / 2 ) { cout << "impossible" << endl ; } else { cout << t << endl ; } } return 0 ; }