蓝桥杯之树状数组和线段树

树状数组

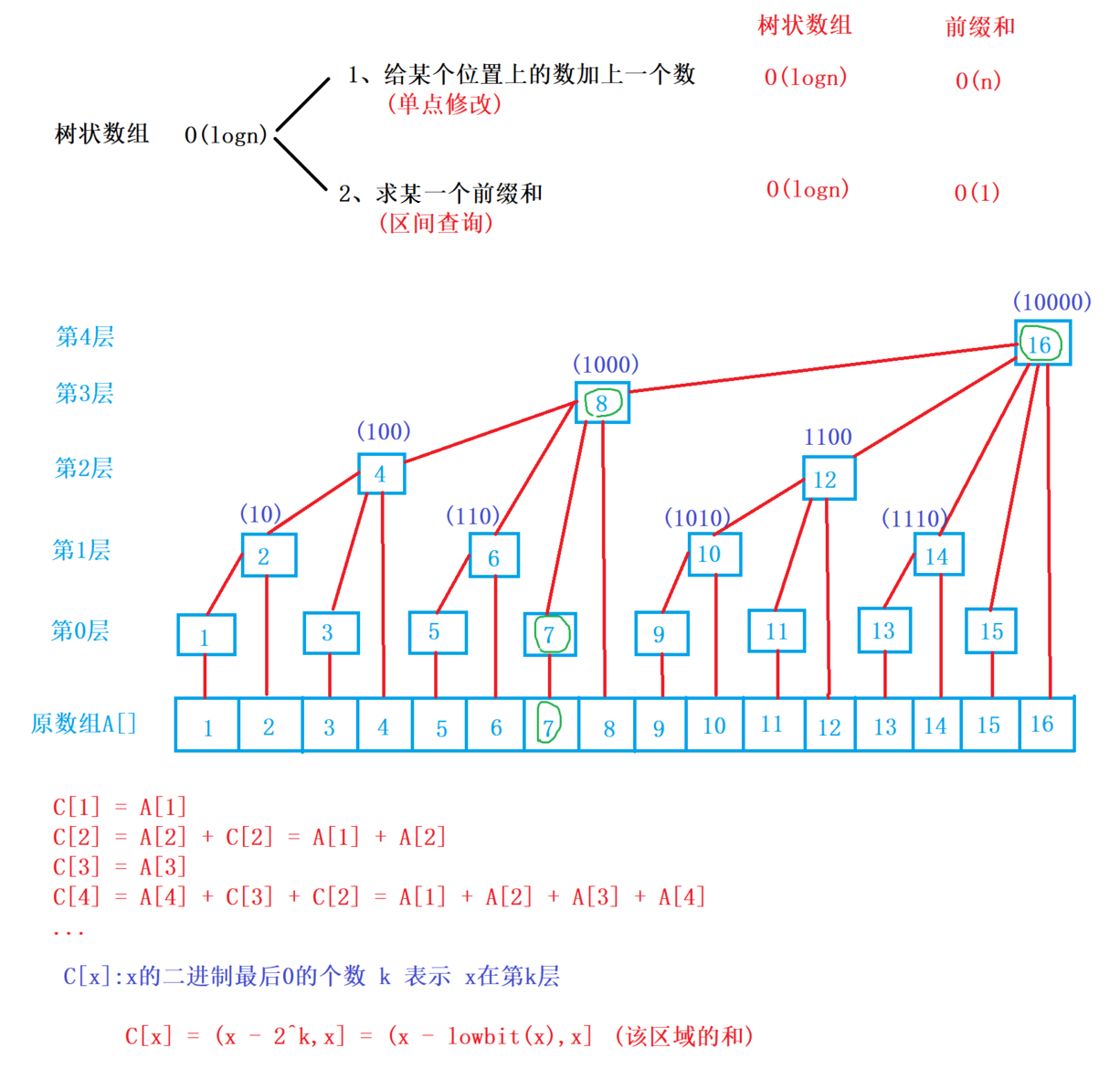
  • lowbit(x):返回x的最后一位1
  • add(x,v):在x位置加上v，并将后面相关联的位置也加上v
  • query(x):询问x的前缀和

1. 动态去连续区间和

给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式

第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。

第二行包含 n 个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b] 的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式

输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围

数据保证在任何时候，数列中所有元素之和均在 int 范围内。

输入样例：

1
2
3
4
5
6
7
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例：

1
2
3
11
30
35

AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int a[N], tr[N];

int lowbit(int x) {
    return x & -x;
}

// 在x位置加上v，并将后面相关联的位置也加上v
void add(int x, int v) {
    for (int i = x; i <= n; i += lowbit(i)) {
        tr[i] += v;
    }
}

int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) {
        res += tr[i];
    }
    
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 1; i <= n; i++) { // 搭建树状数组
        add(i, a[i]);
    }
    
    while (m--) {
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        // k = 0 是询问[x,y]的区间和，k = 1是在x位置添加y元素
        if (k == 0) {
            printf("%d\n", query(y) - query(x - 1));
        }
        else {
            add(x, y);
        }
    }
    
    return 0;
}

2. 数星星

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 kk 颗星星，就说这颗星星是 kk 级的。

1.png

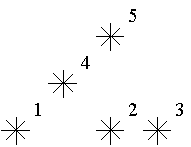
例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。

例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式

第一行一个整数 N，表示星星的数目；

接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；

不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

输出格式

N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

数据范围

输入样例：

1
2
3
4
5
6
5
1 1
5 1
7 1
3 3
5 5

输出样例：

1
2
3
4
5
1
2
1
1
0

AC

1、题目要求求某一个点 (x,y) 左下方星星的个数(不包括自己)，且星星按y坐标增序给出，y 坐标相同的按x坐标增序给出,因此对于每个新来的点 (x,y) ,y 是当前纵坐标的最大值，只需要求[1,x]中星星出现的数量即可

2、通过树状数组完成单点修改，区间查询操作

注意：树状数组是从1开始的，而题目的给定的 x 范围是 0≤x≤32000,因此需要将所有的x赋值成 x + 1(相对位置不变)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 32010;

int n;
int tr[N], level[N]; // tr[] //树状数组, leve[]存各个等级的星星数

int lowbit(int x) {
    return x & -x;
}

void add(int x, int v) {
    for (int i = x; i <= N; i += lowbit(i)) {
        tr[i] += v;
    }
}

int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) {
        res += tr[i];
    }
    
    return res;
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        x++; // 为了防止出现0的情况，给它全体横坐标加上 1
        
        level[sum(x)]++; // 查一下它的前缀和是多少，前缀和是多少就意味着是多少级。这是一个动态变化的过程，而且后面的一定比前面高
        add(x, 1); // 更新一下树状数组，每次都给 x 后面的数据加上 1 
    }
    
    for (int i = 0; i < n; i++) {
        printf("%d\n", level[i]);
    }
    
    return 0;
}

3. 小朋友排队

n 个小朋友站成一排。

现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。

每个小朋友都有一个不高兴的程度。

开始的时候，所有小朋友的不高兴程度都是 0。

如果某个小朋友第一次被要求交换，则他的不高兴程度增加 1，如果第二次要求他交换，则他的不高兴程度增加 2（即不高兴程度为 3），依次类推。当要求某个小朋友第 k 次交换时，他的不高兴程度增加 k。

请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。

如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

输入格式

输入的第一行包含一个整数 n，表示小朋友的个数。

第二行包含 n 个整数 H1,H2,…,Hn，分别表示每个小朋友的身高。

输出格式

输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

数据范围

输入样例：

1
2
3
3 2 1

输出样例：

1
9

样例解释

首先交换身高为3和2的小朋友，再交换身高为3和1的小朋友，再交换身高为2和1的小朋友，每个小朋友的不高兴程度都是3，总和为9。

AC

难点是推算出每个小朋友移动的次数是 k1+k2 是固定的
k1 为小于这个小朋友高度的个数 k2 为大于这个小朋友高度的个数
利用树状数组快速求和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1000010;

int n;
int h[N], tr[N];
int sum[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int v) {
    for (int i = x; i < N; i += lowbit(i)) {
        tr[i] += v;
    }
}

int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) {
        res += tr[i];
    }
    
    return res;
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &h[i]);
        h[i]++; // 身高是从0开始,所以 ++ 从1开始
    }
    
    for (int i = 0; i < n; i++) {
        sum[i] = query(N - 1) - query(h[i]);
        add(h[i], 1);
    }
    
    memset(tr, 0, sizeof tr); // 清空树状数组
    for (int i = n - 1; i >= 0; i--) { // 找出比这个数小的数有多少个，注意这里必须倒着更新，否则无法算出高的层的数值
        sum[i] += query(h[i] - 1);
        add(h[i], 1);
    }
    
    LL res = 0;
    for (int i = 0; i < n; i++) { // 等差数列求和 不高兴度的总和为从1+2+..+sum[i]
        res += (LL)sum[i] * (sum[i] + 1) / 2;
    }
    
    cout << res << endl;
    
    return 0;
}

4. 螺旋折线

如下图所示的螺旋折线经过平面上所有整点恰好一次。

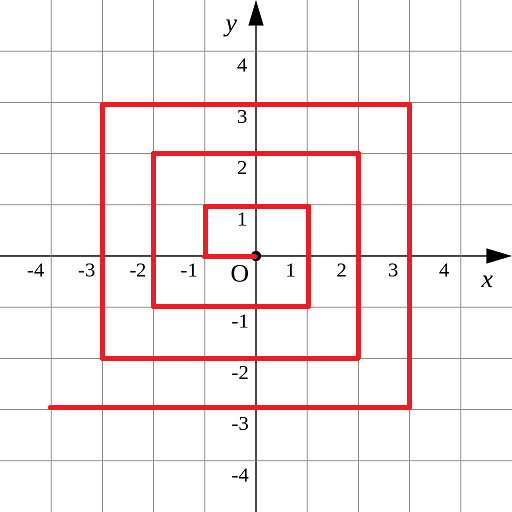
p1.png

对于整点 (X,Y)，我们定义它到原点的距离 dis(X,Y)dis(X,Y) 是从原点到 (X,Y) 的螺旋折线段的长度。

例如 dis(0,1)=3, dis(−2,−1)=9

给出整点坐标 (X,Y)，你能计算出 dis(X,Y)吗？

输入格式

包含两个整数 X,Y。

输出格式

输出一个整数，表示 dis(X,Y)。

数据范围

输入样例：

1
0 1

输出样例：

1
3

AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

int main() {
    int x, y;
    cin >> x >> y;
    
    if (abs(x) <= y) { // 在上方
        int n = y;
        cout << (LL)(2 * n - 1) * (2 * n) + x - (-n) << endl;
    }
    else if (abs(y) <= x) { // 在右方
        int n = x;
        cout << (LL)(2 * n) * (2 * n) + n - y;
    }
    else if (abs(x) <= abs(y) + 1 && y < 0) { // 在下方
        int n = abs(y);
        cout << (LL)(2 * n) * (2 * n + 1) + n - x << endl;
    }
    else { // 在左方
        int n = abs(x);
        cout << (LL)(2 * n - 1) * (2 * n - 1) + y - (-n + 1) << endl;
    }
    
    return 0;
}

线段树

2. 数列区间最大值

输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

输入格式

第一行两个整数 N,M 表示数字的个数和要询问的次数；

接下来一行为 N 个数；

接下来 M 行，每行都有两个整数 X,Y。

输出格式

输出共 M 行，每行输出一个数。

数据范围

数列中的数字均不超过

输入样例：

1
2
3
4
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

输出样例：

1
2
5
8

AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <climits>

using namespace std;

const int N = 100010;

int n, m;
int w[N];
struct Node
{
    int l, r;
    int maxv;
}tr[N * 4];

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;
    int maxv = INT_MIN;
    if (l <= mid) maxv = query(u << 1, l, r);
    if (r > mid) maxv = max(maxv, query(u << 1 | 1, l, r));
    return maxv;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);

    build(1, 1, n);

    int l, r;
    while (m -- )
    {
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, l, r));
    }

    return 0;
}